Voor de vorm
Tegenwoordig is alles te crowdfunden. Ook een schijnbaar curieus gevormd 3D-object zonder duidelijk doel. En hoewel de vorm in kwestie redelijk overbodig lijkt, is hij reuze-interessant.
Het Kickstarterproject Orbiform: A mathematically perfect solid of constant width draait om de productie van zogenoemde orbiforms. Dat blijken 3D-objecten te zijn die niet echt piramidevormig zijn, maar ook zeker niet bolvormig. Het is dan ook een redelijke mindfuck om te zien hoe een plank hout zonder moeite over een aantal orbiforms rolt. Wie dacht dat rollen was voorbehouden aan bollen, ziet zijn wereldbeeld kantelen.
Maar de orbiforms zelf doen eigenlijk helemaal niets: het zijn een soort veredelde presse-papiers. Dat neemt niet weg dat ze populair zijn, want ze hebben hun streefbedrag - dat puur nodig was voor de R&D voor de productie - op het moment van schrijven van deze post ruim vijftien keer bij elkaar gecrowdfund.
Gothische kerkramen
Orbiforms zijn slechts een merknaam. Waar het hier om gaat, is dat het voorwerpen met een constante breedte zijn. Hoe je ze ook draait, ze zijn altijd even breed en hoog. Het bekendste object met een constante breedte is een bol, maar er zijn er dus meer. De tweedimensionale vorm die ten grondslag ligt aan de orbiform wordt meestal aangeduid als de Reuleaux-driehoek, vernoemd naar de negentiende-eeuwse, Duitse werktuigbouwkundig ingenieur Franz Reuleaux.
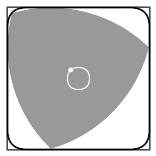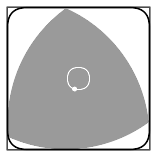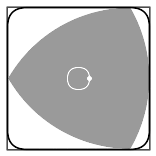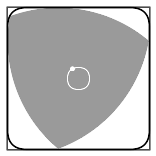
Reuleaux hield zich bezig met het omzetten van de ene soort beweging in de andere en paste de vorm die zijn naam zou gaan dragen veel toe in ontwerpen. Maar de vorm was ruim daarvoor al bekend. Da Vinci gebruikte hem, maar je kunt hem ook kennen van Gothische kerkramen.
Wankelmotor
In het onderstaande filmpje van YouTuber Makers Muse, die uitlegt hoe je een orbiform kunt 3D-printen, krijg je te zien hoe ontzettend simpel de vorm is te maken.
Overigens hoeft de vorm helemaal niet ‘een soort van’ driehoekig te zijn; je kunt dit soort objecten met veel meer hoeken maken. Deze worden Reuleaux-polygonen genoemd. Hoe meer ‘hoeken’ ze krijgen, des te meer ze op een echte bol lijken.
Helaas valt het een beetje tegen wat je met orbiforms kunt. De beroemdste toepassing is de Wankelmotor, maar die telt eigenlijk niet, want de cylinder in de wankelmotor heeft net iets vlakkere zijkanten dan een Reuleaux-driehoek en heeft dus geen constante vorm. Reuleaux-vormen zijn ook niet echt geschikt om een kogellager van te maken, omdat de vormen weliswaar een constante breedte hebben, maar geen volledig centraal zwaartepunt. Kijk maar naar het vervolg van Makers Muse:
De meest functionele toepassingen zijn verder het plectrum (dat plasticje dat gitaristen soms gebruiken om te tokkelen), het potlood dat niet wegrolt én de vierkante-gatenboor. Inderdaad: het gereedschap dat generaties stagiairs op hun eerste dag in de werkplaats moesten gaan zoeken, blijkt gewoon te bestaan: