
Voor de vorm 2: de Gömböc
Nog even over rare vormen dan. Vorige week zagen we de interessante eigenschappen van objecten met constante breedte. Die hadden nog een paar praktische toepassingen. De gekke vorm in dit filmpje kan je helemaal nergens anders voor gebruiken. Maar het wordt wel duidelijk dat mensen een bizar groot brein hebben.
Het object in kwestie heet een gömböc en is mono-monostatisch. Monostatisch wil zeggen dat het slechts één stabiel rustpunt heeft. Het tweede voorvoegsel mono wordt toegevoegd om uit te leggen dat dit object ook maar één onstabiel rustpunt heeft. Dat betekent dat hij altijd terugkeert naar dezelfde positie. En dat is bijzonder, maar je hebt er verder niks aan.
Schokgolven
Lange tijd dacht men dat een vorm als de gömböc niet bestond. Een belangrijke reden daarvoor is dat er in twee dimensies geen convexe (dat wil zeggen: bolle) vorm bestaat die slechts twee evenwichtspunten heeft. Neem de ellips hieronder: die heeft twee stabiele evenwichtspunten en twee instabiele (waar het de vorm dus in principe op gebalanceerd kan worden, maar waar hij makkelijk kan worden ‘omgestoten’).
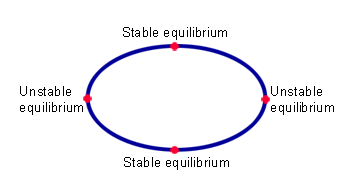
Het blijkt dat het niet mogelijk is om een 2D-vorm te maken die minder dan twee stabiele en twee instabiele evenwichtspunten heeft. Dat is zelfs redelijk makkelijk wiskundig te bewijzen, stelt dit artikel (dat je vooral moet lezen als je meer wilt weten).
Maar in 2006 gingen er schokgolven door de wereld van de wiskunde toen de Hongaarse wetenschapper en ingenieur Gábor Domokos en zijn collega Péter Várkonyi aantoonden dat in de driedimensionale wereld een mono-monostatisch wel degelijk mogelijk was: de gömböc.
Die arme vrouw
Domokos’ zoektocht begon ruim een decennium eerder toen hij werd uitgedaagd door de Russische wiskundige Vladimir Arnold. Die vroeg hem of er een driedemensionaal homogeen (dat wil zeggen: massief) object met minder dan vier evenwichtspunten zou kunnen bestaan. Dat liet Gabór niet op zich zitten. De volgende tien jaar van zijn leven besteedde hij aan vruchteloos onderzoek naar deze mythische vorm. Op een zeker moment dreef hij zijn vrouw tot wanhoop toen hij zelfs op vakantie met de kwestie bezig bleef, en op een kiezelstrand één voor één alle stenen begon te sorteren in de hoop toevallig zo’n object tegen te komen. Gabór en zijn vrouw zijn wonder boven wonder nog bij elkaar, voor zover ik kan nagaan.
Eureka!
De doorbraak kwam toen Gabór ging samenwerken met Péter Várkonyi. Beiden zijn van huis uit geen supersterke wiskundigen, stelt Várkonyi in het filmpje, maar ze vulden elkaar blijkbaar goed aan. ‘It was a fascinating three dimensional puzzle.'
Toen ze uiteindelijk de gömböc-vorm te pakken hadden, was het nog een hele uitdaging om hem te fabriceren. De afmetingen moeten namelijk tot op de honderdste millimeter kloppen, anders werkt het niet. Daarom is de suggestie van comedian Rich Hall, in het filmpje helemaal onderaan, om er een peper en zoutstel van te maken, uiteindelijk niet echt praktisch uitvoerbaar (sowieso zou het geen echte gömböc kunnen zijn, omdat die altijd helemaal massief moeten zijn. Dat zijn nu eenmaal de regels).
En het nut? Wel, anders dan het nastreven van kennis is er geen doel. ‘Westerlingen begrijpen dat niet altijd, maar in het Oosten wordt de schoonheid van het object meer gewaardeerd’. Een leuk feitje: sommige schildpadden hebben een schild in de vorm van een gömböc, zodat ze altijd (zoveel mogelijk in iedere geval) weer op hun pootjes terecht komen.
Stephen Fry
Al met al moesten de wiskundigen flink wat moeite doen om een vorm uit te vinden die alleen nut heeft voor schildpadden. Bovendien vond de evolutie de vorm al een paar miljoen jaar geleden uit. In het onderstaande clipje uit het altijd hilarische wetenschapsprogramma Quite Interesting van de BBC (dat ironisch genoeg niet de juiste beeldverhoudingen heeft) vraag Rich Hall Gábor Domokos dan ook: 'do you feel like you wasted your life?' Maar dan zijn we het toch eens met showhost Stephen Fry: 'You so have not!'







